Symbolica is a computer algebra system which aims to handle expressions with billions of terms, taking up terabytes of diskspace. It can easily be incorporated into existing projects using its Python, Rust or C++ bindings.
For documentation and more, see symbolica.io.
Symbolica allows you to build and manipulate mathematical expressions through matching and replacing patterns, similar to regex for text:

You are able to perform these operations from the comfort of a programming language that you (probably) already know, by using Symbolica's bindings to Python, Rust and C++:
Symbolica is in early development, but can already be used as a library in Rust and Python. The C/C++ bindings allow for fast multivariate polynomial arithmetic.
If you are using Symbolica as a library in Rust, simply include it in the Cargo.toml:
toml
[dependencies]
symbolica = { git = "https://github.com/benruijl/symbolica.git" }
Symbolica can be installed for Python >3.5 using pip:
sh
pip install symbolica
The installation may take some time, as it may have to compile Symbolica.
Alternatively, one can install Symbolica manually. Compile Symbolica with a recent Rust compiler:
sh
git clone https://github.com/benruijl/symbolica.git
cd symbolica
cargo build --release --features python_api
and copy the shared library to your destination location, stripping the leading lib from the filename:
sh
cp target/release/libsymbolica.so symbolica.so
In the following example we create a Symbolica expression (1+x)^2, expand it, and replace x^2 by 6:
python
from symbolica import Expression
x, x_ = Expression.vars('x')
e = (1+x)**2
r = e.expand().replace_all(x**2, 6)
print(r)
which yields 2*x+7.
Variables ending with a _ are wildcards and can match any subexpression.
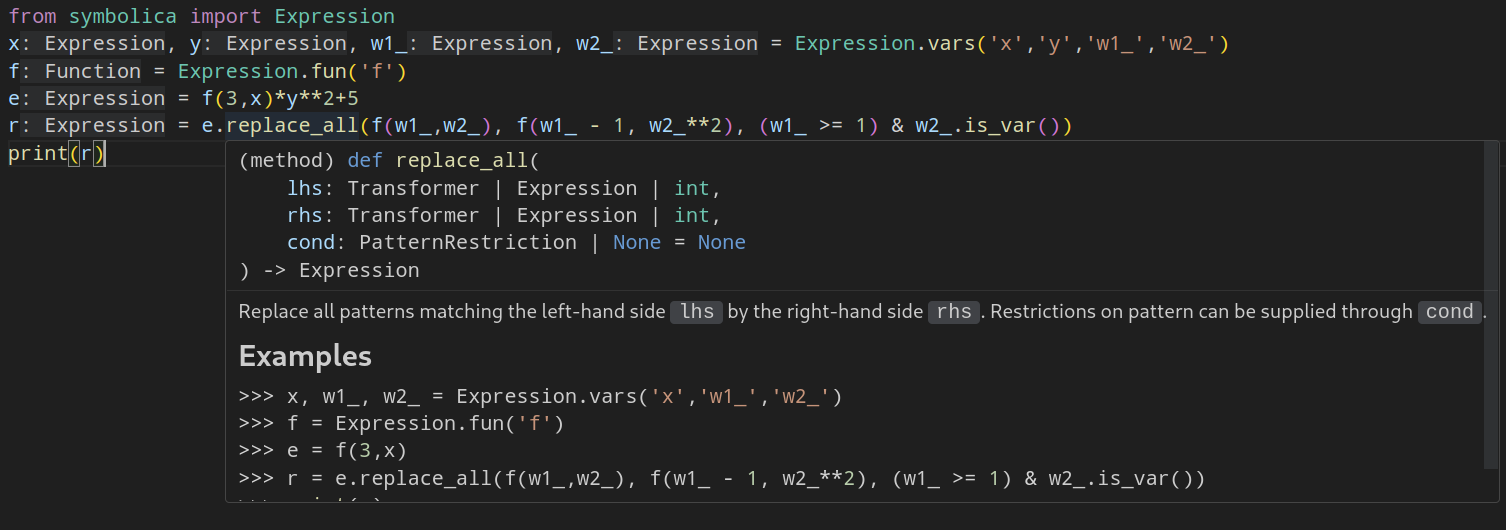
In the following example we try to match the pattern f(w1_,w2_) where w1_ is more than 0 and w2_ must match a variable:
python
from symbolica import Expression
x, y, w1_, w2_ = Expression.vars('x','y','w1_','w2_')
f = Expression.fun('f')
e = f(3,x)*y**2+5
r = e.replace_all(f(w1_,w2_), f(w1_ - 1, w2_**2), (w1_ >= 1) & w2_.is_var())
print(r)
which yields y^2*f(2,x^2)+5.
Symbolica is world-class in rational arithmetic, outperforming Mathematica, Maple, Form, Fermat, and other computer algebra packages. Simply convert an expression to a rational polynomial:
python
from symbolica import Expression
x, y = Expression.vars('x','y')
p = Expression.parse('(x*y^2*5+5)^2/(2*x+5)+(x+4)/(6*x^2+1)').to_rational_polynomial()
print(p)
which yields (45+13*x+50*x*y^2+152*x^2+25*x^2*y^4+300*x^3*y^2+150*x^4*y^4)/(5+2*x+30*x^2+12*x^3).
Follow the development and discussions on Zulip!