A supervised machine learning library for Rust.
If you wish to use Scholar in your project, simply add the following to your Cargo.toml dependencies...
toml
scholar = "0.1"
... then read on to learn about the library's functionality and usage. Note that the following assumes some level of knowledge regarding data science and machine learning.
Datasets are objects used to store the data that you want your ML model to learn. They hold a vector of Rows, which are essentially just a tuple of inputs matched to their expected output. You can construct a dataset either directly or from a CSV file:
```rust // Constructs a dataset directly. // Note that the 'inputs' and 'outputs' are both vectors, even though // the latter has just one element let data = vec![ (vec![0.0, 0.0], vec![0.0]), (vec![0.0, 1.0], vec![1.0]), (vec![1.0, 0.0], vec![1.0]), (vec![1.0, 1.0], vec![0.0]), ];
let dataset = scholar::Dataset::from(data); ```
rust
// Constructs a dataset from a CSV file.
// The second argument indicates that the file doesn't have headers,
// and the third specifies how many columns of the file are inputs
let dataset = scholar::Dataset::from_csv("examples/iris.csv", false, 4)?;
You can split a Dataset into two with the split method. This is useful for separating it into training and testing segments:
rust
// Randomly allocates 75% of the dataset to 'training_data',
// and the rest to 'testing_data'
let (training_data, testing_data) = dataset.split(0.75);
Currently, the library only has functionality for simple neural networks. You can create one like this:
```rust use scholar::{NeuralNet, Sigmoid};
let mut brain: NeuralNet
You must give the network a type annotation so that it knows which activation function to use. You can create your own activations (something that is covered in this section), or you can simply use the in-built sigmoid.
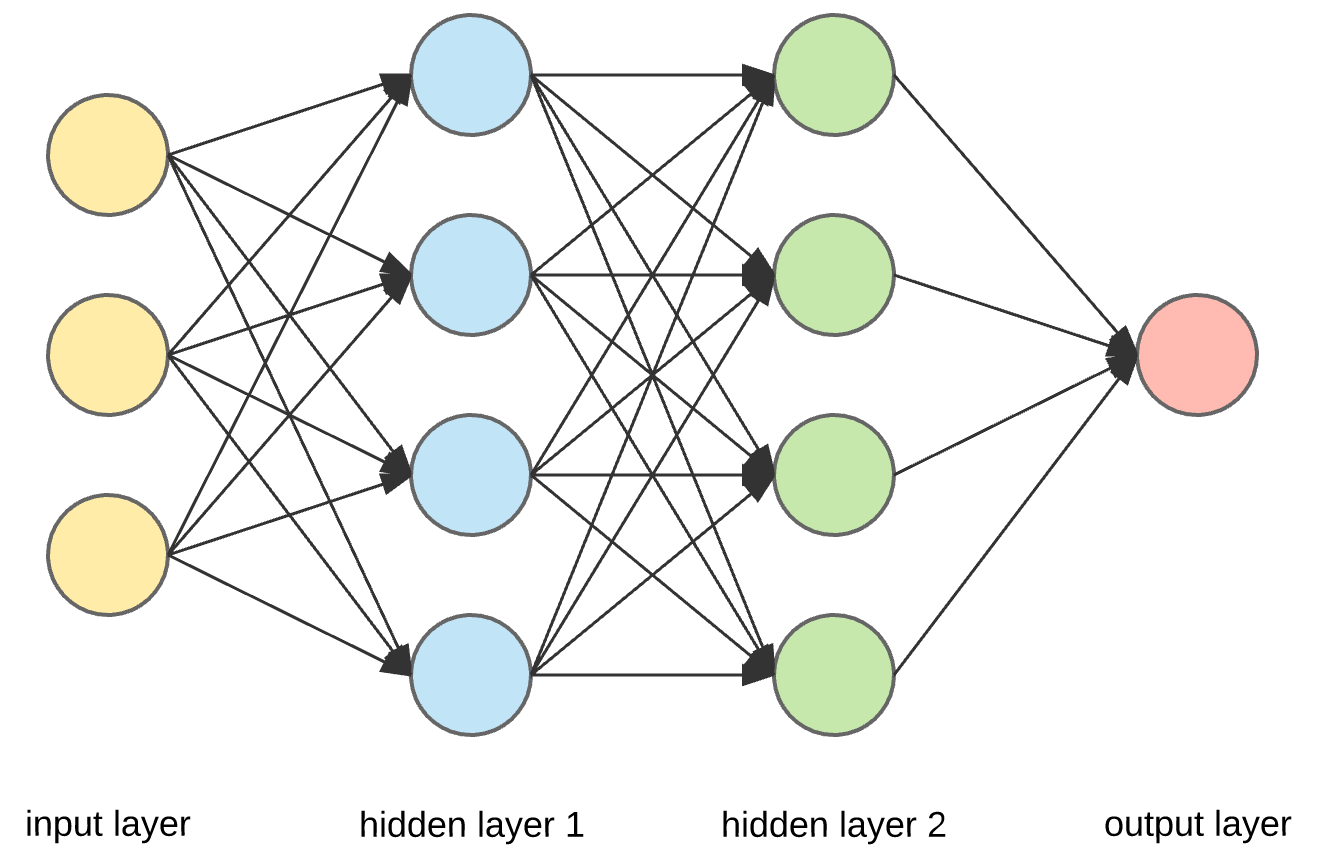
The argument passed to NeuralNet::new is a slice containing the number of nodes (or neurons) that each layer of the network should have. The code above would produce a network like this:

Training and testing a neural network is as easy as it is to create one: just use the train and test methods, respectively:
```rust
let mut brain: NeuralNet
// Trains the network by iterating over the entire dataset 25,000 times. // The last parameter (the 'learning rate') dictates how quickly the network // 'adapts to the dataset' brain.train(yourtrainingdata, 25_000, 0.01);
let averagecost = brain.test(yourtestingdata); println!("Accuracy: {:.2}%", (1.0 - averagecost) * 100.0); ```
It's also very simple to save/load networks to/from files.
```rust
let mut brain: NeuralNet
// Note that the file doesn't have to use the '.network' extension; you can // actually choose anything you wish! brain.save("brain.network")?;
// When loading from a file, you will need to create a new network (or
// shadow an existing one, as is done here)
let mut brain: NeuralNet
In order to create a custom activation for a network, you will need to implement the Activation trait, which requires you to fill in both the regular activation function and the derivative of that function. The code below shows how to implement a simple ReLU activation:
```rust use serde::{Serialize, Deserialize};
// The activation must be serializable and deserializable // so that the network can be saved/loaded to/from files
struct Relu;
impl scholar::Activation for Relu { fn activate(x: f64) -> f64 { x.max(0.0) }
fn derivative(x: f64) -> f64 {
if x > 0.0 {
1.0
} else {
0.0
}
}
} ```
A small quirk with this system appears when an activation's derivative references its regular function, such as in the case with sigmoid (σ). The real derivative of σ(x) is:
σ(x) * (1 - σ(x))
When implementing this in code for a neural network, however, we can simply remove these 'references'. This is because the activation's regular function will have always been applied to the input of its derivative function, no matter the circumstances. The derivative of sigmoid thus becomes:
x * (1 - x)
which matches what the real implementation looks like:
```rust impl Activation for Sigmoid { ...
fn derivative(x: f64) -> f64 {
x * (1.0 - x)
}
} ```
Keep this in mind if you plan on building custom activations.
If at any point you are stuck using this library, be sure to reference the examples (in the examples folder of this repository) or the documentation (at https://docs.rs/scholar/).