
Rust numeric library contains linear algebra, numerical analysis, statistics and machine learning tools with R, MATLAB, Python like macros.
Peroxide provides various features.
default - Pure Rust (No dependencies of architecture - Perfect cross compilation)O3 - SIMD + OpenBLAS (Perfect performance but hard to set-up - Strongly recommend to read OpenBLAS for Rust)plot - With matplotlib of python, we can draw any plots.dataframe - Dataframe & netcdfserde - serialization with Serde.If you want to do high performance computation, then choose openblas feature. If you don't want to depend C/C++ or Fortran libraries, then choose default feature. If you want to draw plot with some great templates, then choose plot feature.
You can choose any features simultaneously.
Peroxide uses 1D data structure to describe matrix. So, it's too easy to integrate BLAS & SIMD. It means peroxide guarantees perfect performance for linear algebraic computations.
Rust is so strange for Numpy, MATLAB, R users. Thus, it's harder to learn the more rusty libraries. With peroxide, you can do heavy computations with R, Numpy, MATLAB like syntax.
For example,
```rust extern crate peroxide; use peroxide::*;
fn main() { // MATLAB like matrix constructor let a = ml_matrix("1 2;3 4");
// R like matrix constructor (default)
let b = matrix(c!(1,2,3,4), 2, 2, Row);
// Or use zeros
let mut z = zeros(2, 2);
z[(0,0)] = 1.0;
z[(0,1)] = 2.0;
z[(1,0)] = 3.0;
z[(1,1)] = 4.0;
// Simple but effective operations
let c = a * b; // Matrix multiplication (BLAS integrated)
// Easy to pretty print
c.print();
// c[0] c[1]
// r[0] 1 3
// r[1] 2 4
// Easy to do linear algebra
c.det().print();
c.inv().unwrap().print();
// and etc.
} ```
Peroxide can do many things.
Vec<f64>fmap : map for all elementscol_map : map for column vectorsrow_map : map for row vectorsReal trait to constrain for f64 and DualNumber structure to unify f64 and Dualrand craterand-dist cratespecial cratepyo3 & matplotlibcsv filesnetcdf filesRust & Cargo are awesome for scientific computations. You can use any external packages easily with Cargo, not make. And default runtime performance of Rust is also great. If you use many iterations for computations, then Rust become great choice.
Corresponding to 0.20.1
O3 feature - Need OpenBLASplot feature - Need matplotlib of pythondataframe feature - Need netcdfcargo.tomltoml
[dependencies]
peroxide = "0.20"
toml
[dependencies.peroxide]
version = "0.20"
default-features = false
features = ["O3"]
toml
[dependencies.peroxide]
version = "0.20"
default-features = false
features = ["plot"]
toml
[dependencies.peroxide]
version = "0.20"
default-features = false
features = ["dataframe"]
toml
[dependencies.peroxide]
version = "0.20"
default-features = false
features = ["O3", "plot", "dataframe"]
mod and re-exportf64, Dual)Vec (Not yet integrated)special craterand crateVec<f64>pyo3)```rust
extern crate peroxide; extern crate inlinepython; use peroxide::*; use inlinepython::python;
fn main() {
// Initial condition
let init_state = State::
let mut ode_solver = ExplicitODE::new(test_fn);
ode_solver
.set_method(ExMethod::RK4)
.set_initial_condition(init_state)
.set_step_size(0.01)
.set_times(1000);
let result = ode_solver.integrate();
let x = result.col(0);
let y = result.col(1);
// Plot (Thanks to inline-python)
python! {
import pylab as plt
plt.plot('x, 'y)
plt.show()
}
}
// dy/dx = (5x^2 - y) / e^(x+y)
fn test_fn(st: &mut State
```rust extern crate peroxide; use peroxide::*;
fn main() {
let init_state = State::
let mut ode_solver = ExplicitODE::new(test_fn);
ode_solver
.set_method(ExMethod::RK4)
.set_initial_condition(init_state)
.set_step_size(0.01)
.set_times(1000);
let result = ode_solver.integrate();
let x = result.col(0);
let y = result.col(1);
// Plot (using python matplotlib)
let mut plt = Plot2D::new();
plt.set_domain(x)
.insert_image(y)
.set_title("Test Figure")
.set_fig_size((10, 6))
.set_dpi(300)
.set_legend(vec!["RK4"])
.set_path("example_data/test_plot.png");
// Remove below comments to activate
//plt.savefig();
}
fn test_fn(st: &mut State
```rust extern crate peroxide; use peroxide::*;
fn main() {
let init_state = State::
let mut ode_solver = ExplicitODE::new(test_fn);
ode_solver
.set_method(ExMethod::RK4)
.set_initial_condition(init_state)
.set_step_size(0.01)
.set_times(1000);
let result = ode_solver.integrate();
let x = result.col(0);
let y = result.col(1);
// Construct DataFrame
let mut df = DataFrame::with_headers(vec!["x", "y"]);
df["x"] = x;
df["y"] = y;
// Write netcdf (Remove below comment)
//df.write_nc("example_data/rk4_test.nc").expect("Can't write nc files");
}
fn test_fn(st: &mut State
```rust extern crate peroxide; use peroxide::*;
fn main() {
let init_state = State::
let mut ode_solver = ExplicitODE::new(test_fn);
ode_solver
.set_method(ExMethod::RK4)
.set_initial_condition(init_state)
.set_step_size(0.01)
.set_stop_condition(stop) // Add stop condition
.set_times(1000);
let result = ode_solver.integrate();
let x = result.col(0);
let y = result.col(1);
let mut plt = Plot2D::new();
plt.set_domain(x)
.insert_image(y)
.set_title("Test Figure")
.set_fig_size((10, 6))
.set_dpi(300)
.set_legend(vec!["RK4"])
.set_path("example_data/test_plot.png");
plt.savefig();
}
fn test_fn(st: &mut State
fn stop(st: &ExplicitODE) -> bool { let y = &st.get_state().value[0]; (*y - 2.4).abs() < 0.01 } ```

```rust extern crate peroxide; use peroxide::*;
// x : n x L // xb: n x (L+1) // v : (L+1) x M // a : n x M // ab: n x (M+1) // w : (M+1) x n // wb: M x N // y : n x N // t : n x N // dh: n x M // do: n x N
fn main() { let v = weightsinit(3, 2); let w = weightsinit(3, 1);
let x = ml_matrix("0 0; 0 1; 1 0; 1 1");
let t = ml_matrix("0;1;1;0");
let y = train(v, w, x, t, 0.25, 5000);
y.print();
}
fn weights_init(m: usize, n: usize) -> Matrix { rand(m, n) * 2f64 - 1f64 }
fn sigmoid(x: f64) -> f64 { 1f64 / (1f64 + (-x).exp()) }
fn forward(weights: Matrix, inputbias: Matrix) -> Matrix { let s = inputbias * weights; s.fmap(|x| sigmoid(x)) }
fn add_bias(input: Matrix, bias: f64) -> Matrix { let b = matrix(vec![bias; input.row], input.row, 1, Col); cbind(b, input) }
fn hide_bias(weight: Matrix) -> Matrix { weight.skip(1, Row) }
fn train( weights1: Matrix, weights2: Matrix, input: Matrix, answer: Matrix, eta: f64, times: usize, ) -> Matrix { let x = input; let mut v = weights1; let mut w = weights2; let t = answer; let xb = add_bias(x.clone(), -1f64);
for _i in 0..times {
let a = forward(v.clone(), xb.clone());
let ab = add_bias(a.clone(), -1f64);
let y = forward(w.clone(), ab.clone());
// let err = (y.clone() - t.clone()).t() * (y.clone() - t.clone());
let wb = hide_bias(w.clone());
let delta_o = (y.clone() - t.clone()) * y.clone() * (1f64 - y.clone());
let delta_h = (delta_o.clone() * wb.t()) * a.clone() * (1f64 - a.clone());
w = w.clone() - eta * (ab.t() * delta_o);
v = v.clone() - eta * (xb.t() * delta_h);
}
let a = forward(v, xb);
let ab = add_bias(a, -1f64);
let y = forward(w, ab);
y
} ```
```rust extern crate peroxide; use peroxide::*;
fn main() {
let noise = Normal(0., 0.5);
let ptrue: Vec
let mut opt = Optimizer::new(data, f);
let p = opt
.set_init_param(p_init)
.set_max_iter(100)
.set_method(LevenbergMarquardt)
.optimize();
p.print();
opt.get_error().print();
let mut plt = Plot2D::new();
plt.set_domain(domain)
.insert_image(y)
.insert_image(p)
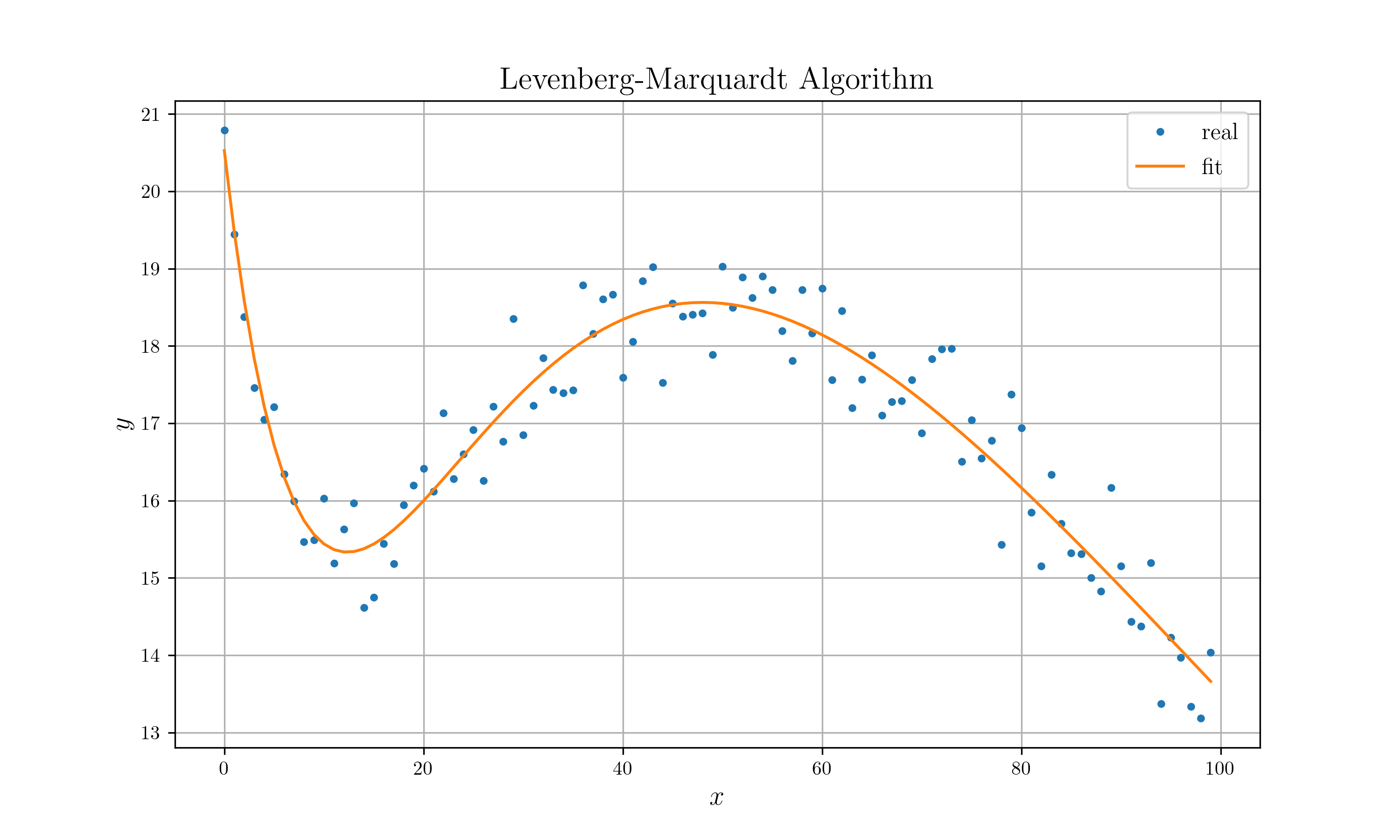
.set_legend(vec!["real", "fit"])
.set_title("Levenberg-Marquardt Algorithm")
.set_path("example_data/lm_test.png")
.set_marker(vec![Point, Line])
.savefig()
.expect("Can't draw a plot");
}
fn f(domain: &Vec
To see RELEASES.md
See CONTRIBUTES.md
To see TODO.md